Buffer Opamp Amplifier

A unity gain buffer amplifier is implemented using an opamp in a negative feedback configuration. The output is connected to its inverting input, and the signal source is connected to the non-inverting input. Although its voltage gain is 1 or unity, it has high current gain, high input impedance and low output impedance. It is used to avoid loading of the signal source.

The output voltage of the op-amp is given by the equation: $$\begin{equation} V_{out} = {A_{OL} \, (V_{\!+} - V_{\!-})} \end{equation}$$ where V+ is the voltage at the non-inverting terminal, V− is the voltage at the inverting terminal and A_OL is the open-loop gain of the amplifier.

Re-arrange the equation $$\begin{equation} {V_{out} \over A_{OL}} = V_{\!+} - V_{\!-} \end{equation}$$

If we assume that A_OL is ∞, then $$\begin{equation} {V_{out} \over A_{OL}} = 0 \end{equation}$$ and substituting equation 3 into equation 2, we obtain $$\begin{equation} V_- = V_+ \end{equation}$$ For negative feedback opamp circuits only, we use equation 4 to simplify the analysis of the circuits.

For this buffer amplifier, using equation 4, we can by inspection obtain $$\begin{equation} V_{out} = V_- = V_+ = V_{in} \end{equation}$$ and derive the gain of the buffer opamp amplifier $$\begin{equation} V_{out} = V_{in} \end{equation}$$

Non Inverting Opamp Amplifier

The non inverting opamp amplifer provides voltage gain. The buffer amplifier can be considered as special case of this amplifer with Rf = 0 and Rg = ∞.

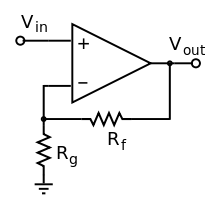
If we let the input current to the inverting input I- = 0 and apply KVL to the Vout, Rf and Rg loop $$\begin{equation} V_- = {V_{out}} {{R_g }\over {R_f + R_g}} \end{equation}$$ Applying equation 4, $$\begin{equation} V_{in} = V_+ = V_- = {V_{out}} {{R_g }\over {R_f + R_g}} \end{equation}$$ Re-arrange the equation to obtain the gain of the non inverting opamp amplifer $$\begin{equation} V_{out} = (1 + {{R_f }\over {R_g}}) {V_{in}} \end{equation}$$