Simple BJT Common Emitter Amplifier
A simple BJT common emitter amplifier is one of three basic single-stage bipolar-junction-transistor (BJT) amplifier topologies. It is used as a voltage amplifier. In this circuit the base terminal of the transistor is the input, the collector is the output, and the emitter is common to both and hence its name.
The simple common emitter amplifier gives the amplifier an inverted output and have a high gain that may vary widely from one transistor to the next. The gain is a function of temperature, bias current and β and so the actual gain is somewhat unpredictable. One common way of alleviating these issues is with the use of emitter degeneration.
- Notes:
- Measure the simulated results and compare with the theoretical ones by using the formulae derived below. You can
obtain the waveform values by moving the cursor within the graph. You may use the following for your
calculations
- VBE = 0.7V
- β = 100
- Note the impact of R1, β and the input signal has on your results. In actual transistors, β can vary by ±50%. The β effect can be eliminated by introducing emitter degeneration.
- We are using the 2N3904 transistor model. If you construct this circuit in the laboratory correctly using the 2N3904 transistor, please note that the actual β of your transistor will affect your measured values.
- Use the Toggle Plot to see the graphs combined or stacked. The stacked plots display maximised waveforms whereas the combined waveforms show their relative values.
DC Analysis
First we redraw the schematic using the BJT DC model. Capacitors are considered open circuit in DC and therefore are excluded.
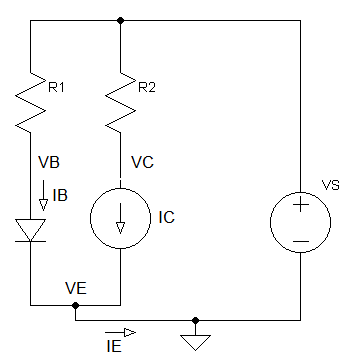
Using KCL (Kirchhoff's current law)
Current through RB
\begin{equation}
I_{R1} = I_B
\end{equation}
Current through RC
\begin{equation}
I_C = \beta I_B
\end{equation}
Current at Node E
\begin{equation}
I_E = I_B + I_C
\end{equation}
Using KVL (Kirchhoff's voltage law) \begin{equation} V_S = I_BR_1 + V_{BE} \end{equation} \begin{equation} V_S = I_CR_2 + V_{C} \end{equation} Substitute equation 2 into equation 5: \begin{equation} V_S = \beta I_BR_C + V_{C} \end{equation}
To obtain maximum output swing, you should choose the resistor values such that VC is half the supply voltage.
\begin{equation} V_{C} = {V_S \over 2} \end{equation}AC Analysis
Next we redraw the schematic using the BJT small signal model. Capacitors are considered shorts in AC and DC supplies are connected to GND (ground). Calculate re
\begin{equation} r_e = {v_T \over I_E} \end{equation}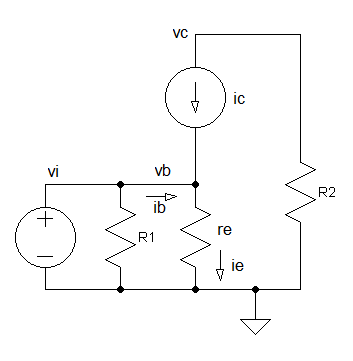
Since the input voltage vi is across re and using ohm's law
\begin{equation} i_e = {v_i \over r_e} \end{equation}The output voltage is \begin{equation} v_c = -i_cR2 \end{equation} the inverted output is due to the current direction.
From KCL we know that \begin{equation} i_e = i_b + i_c \end{equation} By ignoring ib from the equation since it is small compared to ic, we obtain \begin{equation} v_c = -i_eR2 \end{equation}
Applying equation 9 to equation 12, the voltage gain of the amplifier is \begin{equation} {v_c \over v_i} = -{R2 \over r_e} \end{equation}