Ohm's law

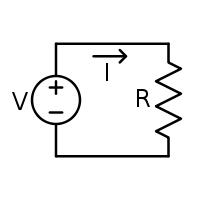
Ohm's law states that the current through a resistor is inversely proportional to the potential difference or voltage across the resistor. The mathematical equation that describes this relationship is

\begin{equation} V = IR \end{equation}

where I is the current in amperes (often shortened to "amps"), V is the potential difference in volts, and R is the resistance (measured in ohms). The potential difference is also known as the voltage drop, and is sometimes denoted by U, E or emf (electromotive force) instead of V.

Resistors in Series

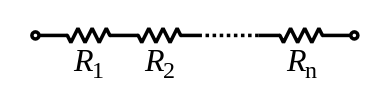
In a series configuration, the current through all of the resistors is the same, but the voltage across each resistor will be in proportion to its resistance. The potential difference (voltage) seen across the network is the sum of those voltages, thus the total resistance can be found as the sum of those resistances.

\begin{equation} R_{eq} = R_1 + R_2 + ... + R_n \end{equation}

Resistors in Parallel

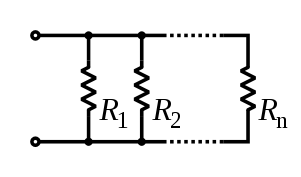
Resistors in a parallel configuration are each subject to the same potential difference (voltage), however the currents through them add. The conductances of the resistors then add to determine the conductance of the network. Thus the equivalent resistance (Req) of the network can be computed,

\begin{equation} {1 \over R_{eq}} = {1 \over R_1} + {1 \over R_2} + ... + {1 \over R_n} \end{equation}

The parallel equivalent resistance can be represented in equations by two vertical lines || as a simplified notation. Occasionally two slashes // are used instead. For the case of two resistors in parallel, this can be calculated using

\begin{equation} R_{eq} = R_1 || R_2 = {R_1 R_2 \over {R_1 + R_2}} \end{equation}