Comparator

A comparator is a device that compares two voltages (or currents) and outputs a digital signal indicating which is larger. It has two analog input terminals V+, and V-, and one binary digital output Vo. It is commonly used in devices that measure and digitize analog signals, such as analog-to-digital converters (ADCs).

$$\begin{equation} if \ V_+ > V_- \ then \ V_{out} = V_{S+} \end{equation}$$ $$\begin{equation} if \ V_- > V_+ \ then \ V_{out} = V_{S-} \end{equation}$$

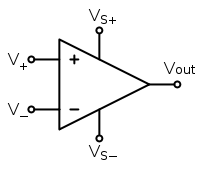
If the output is digital, then V_S+ is H or 1 and V_S- is L or 0. It can then be considered to be a one bit analog to digital converter.

A comparator consists of a specialized high-gain differential amplifier. Due to the high gain, Vout is undetermined for the following condition.

$$\begin{equation} V_- = V_+ \end{equation}$$

A comparator can be implemented using an opamp. The output voltage of the op-amp is given by the equation: $$\begin{equation} V_{out} = {A_{OL} \, (V_{\!+} - V_{\!-})} \end{equation}$$ where A_OL is the open-loop gain of the amplifier.