Inverting Opamp Amplifier

An inverting amplifier inverts and amplifies the input signal. As long as the op-amp gain is very large, the amplifier gain is determined by the external feedback resistor Rf and the input resistor Rin and not by op-amp parameters.

Inverting Amplifier

If we apply KCL to the node at V- (the inverting input) and let the input current to the inverting input be I-, then \begin{equation} {{V_{out} - V_-} \over R_f } + {{V_{in} - V_-}\over R_{in} } = I_- \end{equation} Since the output is connected to V- through Rf, the opamp is in a negative feedback configuration. Thus \begin{equation} V_- = V_+ = 0 \end{equation} And assuming that I- is 0 and simplifying equation 1, \begin{equation} {{V_{out}} \over R_f } + {{V_{in}}\over R_{in} } = 0 \end{equation} Re-arrange the equation to obtain the gain of the inverting opamp amplifer \begin{equation} V_{out} = -{{R_f }\over {R_{in}}} {V_{in}} \end{equation}

Summing Opamp Amplifier

The summing opamp amplifer is a general case of the inverting amplifier with multiple input voltages and resistors.

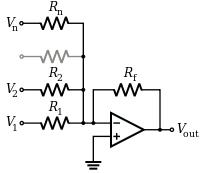
Summing Amplifier

Extending equation 3 to the multiple input voltages and resistors, \begin{equation} {{V_{out}} \over R_f } + {{V_{1}}\over R_{1} } + {{V_{2}}\over R_{2} } + ... + {{V_{n}}\over R_{n} } = 0 \end{equation} Re-arrange the equation to obtain the output voltage of the summing opamp amplifer \begin{equation} V_{out} = -R_f ( {{V_{1}}\over R_{1} } + {{V_{2}}\over R_{2} } + ... + {{V_{n}}\over R_{n} } ) \end{equation} In the case of R1 = R2 = .... = Rn = Rf, the output voltage is the sum of the input voltages \begin{equation} V_{out} = - ( V_{1} + V_{2} + ... + V_{n} ) \end{equation}